Project 1: CryptographyFall 2024

This project counts for 9% of your course grade. Late submissions will be allowed with the use of late days.

This is optionally a group project; you may work in teams of two and submit one project per team. You may also work alone. Note that the final exam will cover project material, so you and your partner should collaborate closely on each part.

The code and other answers you submit must be entirely your team’s own work, and you are bound by the Honor Code. You may discuss the conceptualization of the project and the meaning of the questions, but you may not look at any part of someone else’s solution or collaborate with anyone other than your partner. You may consult published references, provided that you appropriately cite them (e.g., with program comments). Visit the course website for the full collaboration policy.

Starter code is provided via GitHub, and a separate autograder is available to submit your solutions. When you submit, the autograder will also check your code for common errors and provide instant feedback. See “Submission Details” at the end of this spec for instructions about obtaining the starter code and using the autograder. Feel free to modify the starter code to suit your needs—we encourage you to make your solutions as clean and modular as possible.

Your code for this project must be written in Python 3.9.2, which ships with the Docker container for the project. You may only use standard libraries that ship with Python 3 and the custom modules we provide. Note that NumPy and SciPy are not allowed.

You’ll find the online components of this project at https://project1.eecs388.org.

Useful Links

• Docker setup guide
• Starter code
• Part 1 Autograder
• Part 2 Autograder
• Attack Targets

Introduction

In this project, you will investigate vulnerable applications of cryptography, inspired by security problems found in many real-world implementations. In Part 1.1, we’ll guide you through attacking the authentication capability of an imaginary server API by exploiting the length-extension vulnerability of hash functions in the MD5 and SHA families. In Part 1.2, you’ll use a cutting-edge tool to generate MD5 hash collisions, and you’ll investigate how hash collisions can be exploited to conceal malicious behavior in software. In Part 2.1, you’ll perform a chosen ciphertext attack that exploits a padding oracle to decrypt a message without knowing the key. In Part 2.2, you’ll exploit vulnerable RSA padding to forge a digital signature.

Objectives

• Understand common pitfalls when applying cryptographic primitives.
• Investigate how cryptographic failures can compromise the security of applications.
• Appreciate why you should use HMAC-SHA256 as a substitute for common hash functions.
• Understand why padding schemes are integral to cryptographic security.

Part 1

(1.1) Length Extension

In most applications, you should use MACs such as HMAC-SHA256 instead of plain cryptographic hash functions (e.g. MD5, SHA-1, or SHA-256), because hashes, also known as digests, fail to match our intuitive security expectations. What we really want is something that behaves like a pseudorandom function, which HMACs approximate and hash functions do not.

One difference between hash functions and pseudorandom functions is that many hashes are subject to length extension. All the hash functions we’ve discussed use a design called the Merkle-Damgård construction. Each is built around a compression function $f$ and maintains an internal state $s$, which is initialized to a fixed constant. Messages are processed in fixed-sized blocks by applying the compression function to the current state and current block to compute an updated internal state, i.e., $s\_{i+1} = f(s_i, b_i)$. The result of the final application of the compression function becomes the output of the hash function.

A consequence of this design is that if we know the hash of an $n$-block message, we can find the hash of longer messages by applying the compression function for each block $b*{n+1}, b*{n+2}, \ldots$ that we want to add. This process is called length extension, and it can be exploited to attack many applications of hash functions.

Experiment with Length Extension in Python

To experiment with this idea, we’ll use a Python implementation of the SHA-256 hash function, though MD5 and SHA-1 are vulnerable to length extension too. Locate the pysha256 module provided with the starter code, and learn how to use it by running $ pydoc3 pysha256. To follow along with these examples, run Python in interactive mode: $ python3 -i.

Consider the string “Use HMAC, not hashes”. We can compute its SHA-256 hash by running:

from pysha256 import sha256, padding
m = 'Use HMAC, not hashes'.encode()  # .encode() converts str to bytes
h1 = sha256()
h1.update(m)
print(h1.hexdigest())

or, more compactly, print(sha256(m).hexdigest()). The output should be:

8f36ee4a3885bcc8a8446b09e9498808c97667f0266e3641c5d2abca457f9187

SHA-256 processes messages in 64-byte blocks, so, internally, the hash function pads $m$ to a multiple of that length. The padding consists of the byte 0x80, followed by as many 0 bytes as necessary, followed by a 8-byte count of the number of bits in the unpadded message. (If the 0x80 and count won’t fit in the current block, an additional block is added.) You can use the function padding(count) from the pysha256 module to compute the padding that will be added to a count-byte message.

Even if we didn’t know m, we could compute the hash of longer messages of the general form m + padding(len(m)) + suffix by setting the initial internal state of our SHA-256 function to sha256(m), instead of the default initialization value, and setting the function’s message length counter to the size of m plus the padding (a multiple of the block size). To find the padded message length, find the length of m (this can also be guessed by an adversary!) and run padded_message_len = len(m) + len(padding(len(m))).

We need padded_message_len because SHA-256 needs to put a final block of padding after our length-extended message. Since the padding scheme requires a count of the number of bits in the entire message before this final padding block, the current instance of SHA-256 which we are length extending on will not be able to produce the correct padding bytes unless it knows the number of bits “ground up” into the digest (which is passed in as the state argument below).

The pysha256 module lets you specify these parameters as additional arguments to the sha256 object:

h2 = sha256(
    state=bytes.fromhex('8f36ee4a3885bcc8a8446b09e9498808c97667f0266e3641c5d2abca457f9187'),
    count=padded_message_len,
)

Now you can use length extension to find the hash of a longer string that appends the suffix “Good advice”. Simply run:

x = 'Good advice'.encode()  # .encode() converts str to bytes
h2.update(x)
print(h2.hexdigest())

to execute the compression function over x and output the resulting hash. Verify that it equals the SHA-256 hash of m + padding(len(m)) + x, but not that of m + x, which is a common pitfall. Notice that, due to the length-extension property of SHA-256, we didn’t need to know the value of m to compute the hash of the longer string—all we needed to know was m’s length and its SHA-256 hash.

This component was intended to introduce length extension and familiarize you with the pysha256 module; you do not need to submit anything for it.

Conduct a Length Extension Attack

Length extension attacks can cause serious vulnerabilities when people mistakenly try to construct something like an HMAC by using $\text{hash}(\text{secret} \parallel \text{message})$.

The Bank of EECS 388 (which has poor security) hosts a server for controlling its Internet-of-Things (IoT) devices. The server is located at https://project1.eecs388.org/uniqname/lengthextension/.

The server has an API that allows users to perform pre-authorized actions by loading URLs of this form:

https://project1.eecs388.org/uniqname/lengthextension/api?token=token&command=command1&command=command2&...

Bank administrators authorize actions in advance by computing a valid token using a secret 8-byte password. The server checks that token is equal to SHA-256(secret 8-byte password $\parallel$ the portion of the URL starting from the first command=).

Using what you learned in the previous section and without guessing the password, apply length extension to create a URL ending with &command=UnlockSafes that is treated as valid by the server API. You have permission to use the server to check whether your command is accepted. You can verify that your exploit works correctly through the provided endpoint; on success, the web interface will display “Nice work uniqname!“

What to submit

A Python script named len_ext_attack.py that:

1. Accepts an authorized API URL as a command line argument (sys.argv[1]).

2. Modifies the URL so that it will execute the UnlockSafes command.

3. Prints only the modified URL.

You should make the following assumptions:

• The input URL will have a similar form as the examples on the website, but we may change the scheme, port, hostname, and API path, as well as the commands, and the number of commands (although there will be at least one). These values may be of substantially different lengths than in the examples.

• The secret password may be different than in the examples, but it will always be 8 bytes long.

You can find starter code in your GitHub repo. Also, please wrap the URL in double quotes (“) when you test your program. Without them, the part of the URL after the ampersand (&) may become truncated from sys.argv[1]. This is because most Unix shells treat the & character as a command. You should assume the input format given at the top of the starter code:

$ python3 len_ext_attack.py "https://project1.eecs388.org/uniqname/lengthextension/api?token=...."

(1.2) Hash Collisions

MD5 and SHA-1 were once the most widely used cryptographic hash functions, but today they are considered dangerously insecure. This is because cryptographers have discovered efficient algorithms for finding collisions—pairs of messages with the same output values for these functions.

The first known MD5 collisions were announced on August 17, 2004, by Xiaoyun Wang, Dengguo Feng, Xuejia Lai, and Hongbo Yu. Here’s one pair of colliding messages they published:

Message 1:

d131dd02c5e6eec4693d9a0698aff95c 2fcab58712467eab4004583eb8fb7f89
55ad340609f4b30283e488832571415a 085125e8f7cdc99fd91dbdf280373c5b
d8823e3156348f5bae6dacd436c919c6 dd53e2b487da03fd02396306d248cda0
e99f33420f577ee8ce54b67080a80d1e c69821bcb6a8839396f9652b6ff72a70

Message 2:

d131dd02c5e6eec4693d9a0698aff95c 2fcab50712467eab4004583eb8fb7f89
55ad340609f4b30283e4888325f1415a 085125e8f7cdc99fd91dbd7280373c5b
d8823e3156348f5bae6dacd436c919c6 dd53e23487da03fd02396306d248cda0
e99f33420f577ee8ce54b67080280d1e c69821bcb6a8839396f965ab6ff72a70

Convert each group of hex strings into a binary file. (On Linux, run $ xxd -r -p file.hex > file.bin. The Docker container ships with both xxd and openssl.)

1. What are the MD5 hashes of the two binary files? Verify that they’re the same.

   $ openssl dgst -md5 file1.bin file2.bin
   

2. What are their SHA-256 hashes? Verify that they’re different.

   $ openssl dgst -sha256 file1.bin file2.bin
   

This component is intended to introduce you to MD5 collisions. You don’t need to submit anything.

Generating Collisions Yourself

In 2004, Wang’s method took 5 hours to find an MD5 collision on a desktop PC. Since then, researchers have introduced vastly more efficient collision finding algorithms. You can compute your own MD5 collisions using a tool written by Marc Stevens that uses a more advanced technique. The fastcoll tool ships with the Docker container for the project.

1. Generate your own collision with this tool. How long did it take?

   $ time fastcoll -o file1 file2
   

2. What are your files? To get a hex dump, run

   $ xxd -p file
   

3. What are their MD5 hashes? Verify that they’re the same.

4. What are their SHA-256 hashes? Verify that they’re different.

This component is intended to introduce you to fastcoll. You don’t need to submit anything.

SHA-1 has similar vulnerabilities to MD5, but SHA-1 collisions are more expensive to compute. The first SHA-1 collision was published in 2017 and took 110 GPU-years to compute. Another attack, published on Jan. 7, 2020, computed a SHA-1 collision with arbitrary prefixes on a GPU cluster at a cost of about $75,000. These costs are likely to fall dramatically as the collision algorithms improve.

A Hash Collision Attack

The collision attack lets us generate two messages with the same MD5 hash and an arbitrary but identical prefix. (More expensive attacks allow generating collisions with different chosen prefixes.) Due to MD5’s length-extension behavior, we can append any suffix to both messages and know that the longer messages will also collide. This lets us construct files that differ only in a binary “blob” in the middle and have the same MD5 hash, i.e. $\textit{prefix} \parallel \textit{blob}\_A \parallel \textit{suffix}$ and $\textit{prefix} \parallel \textit{blob}\_B \parallel \textit{suffix}$.

We can leverage this to create two programs that have identical MD5 hashes but arbitrarily different behaviors. We’ll use Python 3, but almost any language would do. Put the following three lines into a file called prefix, followed by an empty line:

#!/usr/bin/python3
# coding: latin-1
blob = """

and put these three lines into a file called suffix, preceded by an empty line:

"""
from hashlib import sha256
print(sha256(blob.encode("latin-1")).hexdigest())

Now use fastcoll to generate two files with the same MD5 hash that both begin with prefix ($ fastcoll -p prefix -o col1 col2). Then append the suffix to both ($ cat col1 suffix > file1.py; cat col2 suffix > file2.py).

Verify that file1.py and file2.py have the same MD5 hash but generate different output. If they generate the same output, it’s possible that Python has been confused by the collision that was generated. Try running fastcoll again to generate a new col1 and col2, then append them to the suffix again.

Extend this technique to produce a pair of programs, good.py and evil.py, that have identical MD5 hashes.

good.py should execute a benign payload: print("Use SHA-256 instead!").
evil.py should execute a pretend malicious payload: print("MD5 is perfectly secure!").

Ensure that your programs output only these messages, and that they exactly match what is specified.

After generating a collision and placing the blobs inside Python triple-quoted strings, there is a chance you will encounter an error saying “EOF while scanning triple-quoted string literal”. Sometimes, when fastcoll generates the blobs, they may contain null bytes or escape sequences that are not interpreted nicely by Python when encoding. Running fastcoll again to obtain a different set of blobs should alleviate this issue.

What to submit

Two Python scripts named good.py and evil.py that:

1. Have identical MD5 hashes.

2. Have different SHA-256 hashes.

3. Print different messages, as specified above.

Note that we may rename these programs before grading them. Furthermore, ensure that your usage of whitespace is consistent across good.py and evil.py! Whitespace characters (spaces, tabs, and newlines) change the binary representation of the file just like any other character, and could lead to your MD5 hashes being different when you expected them to be identical.

Part 2

(2.1) Padding Oracle Attack

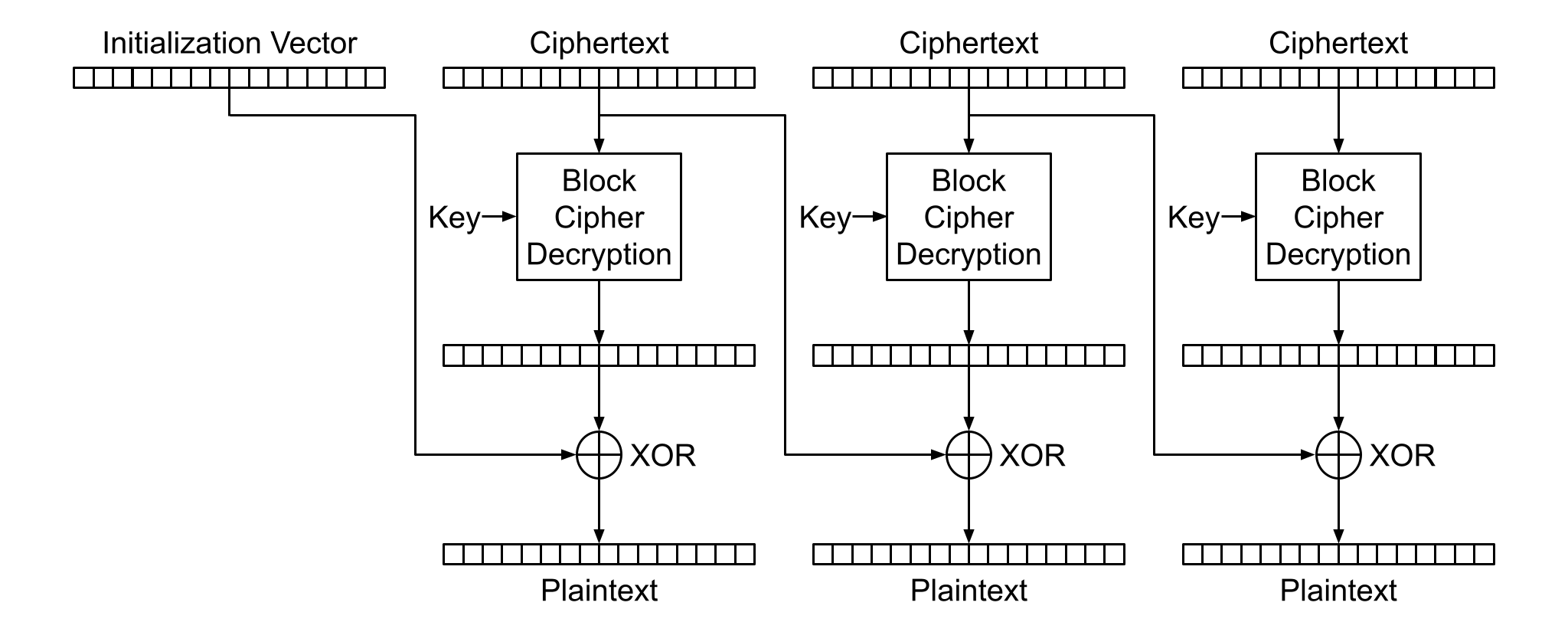
Cipher-Block Chaining, or CBC, is a block cipher mode of encrypting variable length inputs. When encrypting with CBC mode, each plaintext block is XORed with the previous ciphertext block before being encrypted. This also means that when decrypting, each block of plaintext is generated by being XORed with the previous block of ciphertext, as seen in the figure above.

In order for the message to be a multiple of the block length, CBC mode uses a padding scheme. PKCS #7 defines a standard for padding the message to the necessary length, in which the final block is filled with $B$ bytes, each with the value $B$. For example, if the block size is 16 bytes and your message only fills 12 bytes of the last block, the final 4 bytes will be padded with (0x04, 0x04, 0x04, 0x04). To avoid ambiguity, if the message length is an exact multiple of the block size, a full block of padding is appended (that is, 16 bytes of 0x10).

Padding Oracle Attacks

After decrypting the ciphertext, the receiver strips off the padding to return the original message. But what happens the receiver finds that the padding is malformed? For example, the last block might end in (0x03 0x02). In that case, their crypto library will likely return an error.

In a client-server scenario where the server is supposed to decrypt the message but keep the message content secret, a padding oracle vulnerability exists if the server indicates to the client that the padding was invalid. In this case, it is possible for an attacker to interactively query the server with manipulated copies of the ciphertext until the padding error does not occur, allowing them to determine, byte-by-byte, what the plaintext contains without knowing the key!

To prevent padding oracle attacks, implementations should check the integrity of the ciphertext using a MAC before decrypting it. Older implementations often decrypt first, then check a MAC, which easily leads to this vulnerability (and the Cryptographic Doom Principle!).

Exploit a CBC Padding Oracle

In our relentless pursuit of justice, we’ve discovered a website containing dead drops—a place where spies leave anonymous, encrypted messages for other spies to later retrieve. It is located at https://project1.eecs388.org/uniqname/paddingoracle/.

To an encrypt a message $m$, the sending spy computes:

$c=\text{AES128-CBC-Encrypt}_{k_1}(m\parallel \text{HMAC-SHA256}_{k_2}(m))$

$\text{AES128-CBC-Encrypt()}$ pads the input as described above.

The site has a form that allows the spies to test whether messages can be properly decrypted. The form uses JavaScript to make an HTTP GET request to this URL: https://project1.eecs388.org/uniqname/paddingoracle/verify?message=message

Your task is to create a program that can use the site as a padding oracle to decipher the messages.

Agent Kerckhoffs has conducted some preliminary analysis that may be useful. He has written some Python representing what we suspect the server does when the /verify endpoint is accessed:

from Crypto.Cipher import AES
from Crypto.Hash import HMAC, SHA256
from Crypto.Random import get_random_bytes

def pad(message):
    n = AES.block_size - len(message) % AES.block_size
    if n == 0:
        n = AES.block_size
    return message + bytes([n]*n)

def unpad(message):
    n = message[-1]
    if n < 1 or n > AES.block_size or message[-n:] != bytes([n]*n):
        raise Exception('invalid_padding')
    return message[:-n]

def encrypt(message, key):
    iv = get_random_bytes(AES.block_size)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    return iv + cipher.encrypt(pad(message))

def decrypt(ciphertext, key):
    if len(ciphertext) % AES.block_size:
        raise Exception('invalid_length')
    if len(ciphertext) < 2 * AES.block_size:
        raise Exception('invalid_iv')
    iv = ciphertext[:AES.block_size]
    cipher = AES.new(key, AES.MODE_CBC, iv)
    return unpad(cipher.decrypt(ciphertext[AES.block_size:]))

def hmac(message, mac_key):
    h = HMAC.new(mac_key, digestmod=SHA256)
    h.update(message)
    return h.digest()

def verify(message, mac, mac_key):
    if mac != hmac(message, mac_key):
        raise Exception('invalid_mac')

def macThenEncrypt(message, key, mac_key):
    return encrypt(message + hmac(message, mac_key), key)

def decryptThenVerify(ciphertext, key, mac_key):
    plaintext = decrypt(ciphertext, key)
    message, mac = plaintext[:-SHA256.digest_size], plaintext[-SHA256.digest_size:]
    verify(message, mac, mac_key)
    return message

@app.route('/verify', methods=['POST'])
def dec_oracle_route():
    ciphertext = bytes.fromhex(request.form['message'])
    try:
        decryptThenVerify(ciphertext, KEY, MAC_KEY)
    except(e):
        return {'status': e}
    return {'status': 'valid'}

What to submit

A Python script called padding_oracle.py that:

1. Accepts two command-line arguments: the oracle URL (sys.argv[1]) and the hex-encoded encrypted message (sys.argv[2]).

2. Uses the provided URL as a padding oracle to decrypt the message.

3. Prints only the decrypted message, as human-readable text (not hex). Don’t print the MAC or the padding.

You can find starter code in the your GitHub repo.

You have permission to use the following oracle URL to decipher the messages: https://project1.eecs388.org/uniqname/paddingoracle/verify

However, do not hard-code the URL, as we will use a different endpoint for grading.

(2.2) RSA Signature Forgery

A secure implementation of RSA encryption or digital signatures requires a proper padding scheme. RSA without padding, also known as textbook RSA, has several undesirable properties. One property is that it is trivial for an attacker with only an RSA public key pair $(n,e)$ to produce a mathematically valid $(\text{message}, \text{signature})$ pair by choosing any signature $s$ and returning $(s^e, s)$.

In order to prevent an attacker from being able to forge valid signatures in this way, RSA implementations use a padding scheme to provide structure to the values that are encrypted or signed. The most commonly used padding scheme in practice is defined by the PKCS #1 v1.5 standard.

Validating RSA Signatures

You can experiment with validating RSA signatures yourself using the openssl toolkit. Create a text file called key.pub that contains the following RSA public key:

-----BEGIN PUBLIC KEY-----
MFowDQYJKoZIhvcNAQEBBQADSQAwRgJBALvMZ+YhjwKpteNYzzbPHvPqdvMrs2Rf
HeIhK+ui9v0YHNyFW6aBwwG/6sfbvxx4OlePBWjRhpoxDC5A/J+rVXkCAQM=
-----END PUBLIC KEY-----

Confirm that the key has a 512-bit modulus with an exponent of 3. You can view the modulus and public exponent of this key by running:

$ openssl rsa -in key.pub -pubin -text -noout

Create a file containing only the text EECS 388 rul3z! ($ echo -n 'EECS 388 rul3z!' > myfile). The following is a base64-encoded signature of the file using the private key corresponding to the public key above.

cEnO8WBePTdtCV6DXudzecMMl60N2cZdJjoIZCK/ir/zsuF1GPFp1yoLrA/NO2LZ
FZOC4IpP5tjyDeYizYqoRg==

Copy the base64-encoded signature to a file named sig.b64, and then convert it from base64 to raw bytes ($ base64 --decode -i sig.b64 > sig). Verify the signature against the file you created:

$ openssl dgst -sha256 -verify key.pub -signature sig myfile

We can also use basic math operations in Python to explore this signature further. Remember, RSA ciphertexts, plaintexts, exponents, moduli, and signatures are actually all integers.

Usually, you would use a cryptography library to import a public key. However, for the purposes of this part of the assignment, you can just manually assign the modulus and exponent as integers in Python based on the earlier output from OpenSSL. You may find the following command useful:

$ openssl rsa -in key.pub -text -noout -pubin | egrep '^ ' | tr -d ' :\n'

Launch Python in interactive mode ($ python3 -i) and assign the modulus and the exponent to integer variables:

# n is the modulus from the key.
# You can just assign it as a hexadecimal literal--remember to start with 0x
# It will look something like:
>>> n = 0x00bbcc67e6218f02a9 ... fc9fab5579

# e is the exponent from the key
>>> e = 3

We can also load the signature into Python. Like the modulus and the exponent, we’ll convert the signature to an integer:

>>> import base64
>>> signature = open('sig.b64').read()
# decode and convert to hexadecimal integer
>>> signature = int.from_bytes(base64.b64decode(signature), byteorder="big")

Now reverse the RSA signing operation by computing $\texttt{signature}^\texttt{e} \bmod \texttt{n}$:

>>> pkcs = pow(signature, e, n)

You can print the resulting value as a 64-byte (512-bit) integer in hex:

>>> f'{pkcs:0128x}'

You should see something like 0001fffff…9baf336a45e7a58f5fddbdc8ba2fa.

Verify that the last 32 bytes of this value match the SHA-256 hash of your file:

>>> import hashlib
>>> m = hashlib.sha256()
>>> m.update(b"EECS 388 rul3z!")
>>> m.hexdigest()

The hash has been padded using the PKCS #1 v1.5 signature scheme to produce the pkcs variable you computed earlier. The signature scheme specifies that, for a SHA-256 hash with a $k$-bit RSA key, the value to be signed, and later verified against, will contain the following bytes:

The number of FF bytes varies such that the size of the result is equal to the size of the RSA key. Confirm that the value of pkcs you computed above matches this format.

It is crucial for implementations to verify that every bit is exactly as it should be, but sometimes developers can be lazy…

Bleichenbacher’s Attack

It’s tempting for a programmer to validate the signature padding as follows: (1) confirm that the total length equals the key size; (2) strip off the bytes 00 01, followed by any number of FF bytes, then 00; (3) parse the ASN.1 bytes; (4) verify that the next 32 bytes are the correct SHA-256 digest.

This procedure does not check the length of the FF bytes, nor does it verify that the hash is in the least significant (rightmost) bytes of the string. As a result, it will accept malformed values that have “garbage” bytes following the digest, like this example, which has only one FF:

Convince yourself that this value would be accepted by the incorrect implementation described above, and that the bytes at the end labeled YY would be ignored. When an implementation uses this lenient, incorrect parsing, an attacker can easily create forged signatures that it will accept.

This possibility is particularly troubling when RSA is used with $e = 3$. Consider the case with RSA encryption: If we encrypt an unpadded message $m$ that is much shorter than $k$-bits, then $m^3 < n$. Thus, the “encrypted” message $c = m^e = m^3 \bmod n$ does not “wrap around” the modulus $n$. In this case, RSA doesn’t provide good security, since the attacker can simply take the normal cube root of the ciphertext to find the plaintext, $m = c^{1/3}$. It’s easy to reverse normal exponentiation, as opposed to modular exponentiation!

Now recall that RSA signature validation is analogous to RSA encryption. If the signature uses $e=3$, the validator calculates $s^e = s^3 \bmod n$ and checks that the result is the correct PKCS-padded digest of the signed message.

Here comes the attack: For a 2048-bit key, a correctly padded value for an RSA signature using a SHA-256 hash should have $k/8 - 54 = 2048/8 - 54 = 202$ bytes of FFs. But what if there were only one FF, as in the example shown above? This would leave space for 201 arbitrary bytes at the end of the value. The weak implementation described above would ignore these bytes.

To construct a signature that would validate against such an implementation, the attacker needs to find a number $x$ such that $x^3 < n$ and where $x^3$ matches the format of the malformed example shown above. To do this, you can construct an integer whose most significant bytes have the correct format, including the digest of the target message, and set the last 201 bytes to 00. Then take the cube root, rounding as appropriate.

Constructing Forged Signatures

The Bank of EECS 388 lets customers send each other money using their digital signatures through a site at https://project1.eecs388.org/uniqname/bleichenbacher/.

To authorize a transfer, the sender makes a digital signature on a message that consists of: from_uniqname+to_uniqname+amount

The recipient enters the account names, amount, and signature into the bank site, which verifies the signature to confirm the transfer.

Unfortunately, the bank uses an old crypto library that is vulnerable to Bleichenbacher’s signature forgery attack. Your task is to construct a program that can forge valid signatures, in order to demonstrate how attackers could fool the bank into making unauthorized transfers to their accounts.

What to submit

A Python script called bleichenbacher.py that:

1. Accepts the transfer message to be signed as a command line argument (sys.argv[1]).

2. Prints only a base64-encoded forged signature of the input string.

You have our permission to use the Bank of EECS 388 to test your signatures, but when we grade your program it will not have access to the network.

You should make the following assumptions:

• The sender’s public key is 2048 bits long and uses $e=3$.

You can find starter code in your GitHub repo. We have also provided a Python library, roots.py, that provides several functions you may wish to use when implementing your solution. To examine its documentation, run $ pydoc3 roots.

Submission Details

1. Create a repo using the GitHub template. Make sure that the repo you create is private.

2. Check that your repo contains the following starter files and directories:

3. Logistics: .devcontainer, .vscode, and .gitignore (all hidden by default), README.md

4. 1.1: len_ext_attack.py, pysha256.py

5. 1.2: evil.py, good.py

6. 2.1: padding_oracle.py

7. 2.2: bleichenbacher.py, roots.py

8. By each deadline, make sure your work is submitted to the appropriate autograder.

Part 1 autograder Part 2 autograder

Although the autograder submission screen shows the 6 p.m. deadline, you can still submit after this time using late days. Any submissions after the posted deadline will use late days, even if your best submission occurred before the deadline. The autograder will not warn you of this. (You don’t get to attempt a higher score after the deadline with no risk.)

Ensure the following items are completed and submitted by the deadline:

Part 1

• len_ext_attack.py
• good.py
• evil.py

Part 2

• padding_oracle.py
• bleichenbacher.py

Once you’re done with the project, you can delete the project 1 Docker container to reclaim resources on your computer. Don’t delete the entire Docker installation (you’ll need it for future projects), just the container.